Vector
before we explain Vector Cosine Similarity, we briefly brush over what a vector is to get everybody on the same page.A vector is a sequence of numbers of arbitrary length(a.k.a dimensions), for example, a vector of dimension 2, with sequence [3,1] could be plotted on a piece of paper.
a vector with dimension 3, and sequence [3,1,1]could be plotted in a 3d projection like so, however higher dimensions are difficult to imagine, but know they could be much larger than 3
We observe that a vector has a length(a.k.a) and a direction. The length is calculated with the Pythagorean algorithm :
Now that we are vector experts, let us dig a bit deeper into the similarity of vectors,
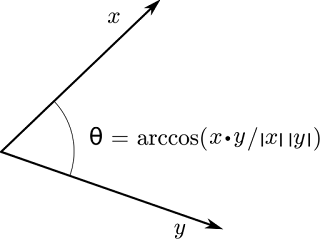
The angle between 2 vectors can be calculated with some vector math described in the following image:
Vector Cosine Similarity
When a vector is equal to another vector, it means their sequences are equal. This means they have the same length and the same direction. When a vector is similar it has roughly the same length and direction.The angle between 2 vectors can be calculated with some vector math described in the following image:
where x.y is the dot product and |x|,|y| is the length of the vector x,y respectively.
We see that if the angle gets smaller we get an indication the vectors have a similar direction.
This gives us a nice metric to detect if 2 vectors are similar.
Vector Cosine Similarity Usecases
Vector Cosine Similarity Usecases
what can we do with this metric, simply put if we can translate data to a vector we can detect its similarity to other data.
Semantic Search
For searching documents, normally the text is indexed in split up into separate parts (n-grams), so partial word matching would find a match.
However, if we index the sentence: "the fox jumped over the fence", the query match on the search term "animal", would not yield any search results, "animal" would only give a result if it was added manually as a synonym to the search index of that document.
However, if we index the sentence: "the fox jumped over the fence", the query match on the search term "animal", would not yield any search results, "animal" would only give a result if it was added manually as a synonym to the search index of that document.
With Word2Vec we can translate the document into a set of vectors. These vectors are stored and when comparing the query->Word2Vec and do a similarity search on these stored vectors.
Speaker Recognition
Similarly, when audio is translated to speaker-specific vectors, the same approach could be applied to identify the previously-stored audio of speakers for identification.
Face Recognition
Similarly, facial features are transformed into a set of vectors, which enables us to search for similar features.
We will explore the semantic search in an upcoming blog





0 Comments
Post a Comment